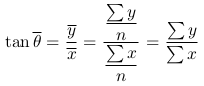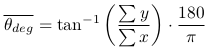風向と風速の計算について – ベクトル平均

Tweet

　実投入したWeather Meters だが、これで観測される風向および風速については、あくまでもその瞬間のデータとなる。だが、いわゆる「風向」「風速」とは瞬間風向、瞬間風速のことではなく、10分間の平均風向・風速を指すらしい。

　ここで問題がひとつある。風向、風速とは平たく言えば風の単位ベクトルとスカラーのことであり、風速はともかく風向の平均とはベクトル平均のことになる。算術平均を計算してしまうと、例えば 350 度と 10 度の平均は 0 度になるべきなのに 180 度になってしまい、全く正反対の結果になる。角度の平均については「角度の平均、角度の分散について」が詳しいが、気象庁では単位ベクトル平均で計算しているらしい。なので、今回は単位ベクトル平均で計算したい。とりあえずお手軽に Ruby + SQLite3 で書いてみた。

　まず、いわゆる風向は 0 ≦ θ < 360 の度数法で得られるが、単位ベクトルを計算するために三角関数を使う必要があり、Ruby の Math モジュールの引数はラジアンなのでラジアンに変換する必要がある。これは単純計算で

になる。次に、角度を単位ベクトルに変換するわけだが、要は半径 1 の円周上の点になるので

これで各ベクトル成分が求まるので、これを成分ごとに算術平均を計算すればいい。ただ、Weather Meters の風向については単純に 16 方位しか取れない。そのため、風向のデータをその場で単位ベクトル化するのではなく、予め計算したテーブルで変換したほうが負荷が少ない。

UNIT_VECTOR_TABLE = {
  -1.0   => [ nil, nil ],
  0.0   => [ 1.0, 0.0 ],
  22.5  => [ 0.923879532511287, 0.38268343236509 ],
  45.0  => [ 0.707106781186548, 0.707106781186547 ],
  67.5  => [ 0.38268343236509,  0.923879532511287 ],
  90.0  => [ 0, 1.0 ],
  112.5 => [ -0.38268343236509,  0.923879532511287 ],
  135.0 => [ -0.707106781186547, 0.707106781186548 ],
  157.5 => [ -0.923879532511287, 0.38268343236509 ],
  180.0 => [ -1.0, 0 ],
  202.5 => [ -0.923879532511287, -0.38268343236509 ],
  225.0 => [ -0.707106781186548, -0.707106781186547 ],
  247.5 => [ -0.38268343236509,  -0.923879532511287 ],
  270.0 => [ 0, -1.0 ],
  292.5 => [ 0.38268343236509,  -0.923879532511287 ],
  315.0 => [ 0.707106781186547, -0.707106781186548 ],
  337.5 => [ 0.923879532511287, -0.38268343236509 ]
}

後で平均を求める必要があるので、このデータは計測ごとに SQLite などの DB に保存しておく。

　次に単位ベクトル平均を取って角度に戻すわけだが、ベクトル成分を角度に戻すにはタンジェントを取ればいい。タンジェントは X 成分 ÷ Y 成分なので

となり、平均ではなく合計だけ計算すればいいことになる。浮動小数点演算を重ねれば重ねるほど誤差が大きくなるので、あくまで合計を計算するだけにしたほうがいい。

　タンジェントが計算できれば、あとはタンジェントの逆関数で角度に戻し、ラジアンから度数法に戻す。

　これで角度が求められるが、得られた値については以下の問題がある。

• タンジェントは -90 度 〜 90 度の 180 度で得られる。
• 180 度ごとに発散してしまうので、別途置き換える必要がある。
• X 成分が負のとき = 90度 〜 270 度のときは求められた角度に 180 を足す必要がある。
• 浮動小数点演算の誤差を考慮する必要がある。

　誤差については最終的に 16 方位に落とせればいいので厳密に考える必要はない。発散については、それを考慮してくれる Math.atan2 があるのだが、値域の関係で使いづらいので Math.atan で計算する。なので、それを踏まえて

# 丸め
x  = (x * 10000).to_i.to_f / 10000.0
y  = (y * 10000).to_i.to_f / 10000.0
direction = 0.0
# 発散する場合またはtan = 0
if x == 1 && y == 0
  direction = 0
elsif x == -1 && y == 0
  direction = 180
elsif x == 0 && y == 1
  direction = 90
elsif x == 0 && y == -1
  direction = 270
else
# arctan から度数に落とす
  direction = ((Math.atan2(y, x) * 180 / Math::PI) + (x < 0 ? 180 : 0)) % 360
end

となるだろうか。ただし、変数 x, y にはそれぞれ X 成分と Y 成分の合計が入っているものとする。

　こんな感じで風向の平均が計算できた。風速については単純にスカラー平均なので、得られた風速のデータを算術平均すればいい。

Tweet